类数值方法PNDM：Stable Diffusion默认加速采样方案（满满干货）数值的方法，

原副标题：类值形式PNDM：Stable Diffusion预设快速取样计划

©PaperWeekly 原创 · 作者 | 刘路平

单位 |南京大学

科学研究方向 | 蔓延数学模型

蔓延数学模型 [1]（diffusion model）透过逐渐插值的形式创建起概率分布和曲线插值的相关联，将深度聚合数学模型提升到了捷伊高度。蔓延数学模型聚合结论的技术细节准确度和样品丰富度都给人留下了深刻的第一印象。

不过，蔓延数学模型须要成千上万次的插值来获得最后的结论，巨大的计算开支妨碍了蔓延数学模型的应用领域和破冰。他们剖析蔓延数学模型的插值式子，透过导入值预测中的低阶值形式，并与蔓延数学模型中的无乱数项插值法（DDIM）相结合，设计出适合蔓延数学模型的低阶快速插值形式。

在今年的 ICLR 2022 上，他们提出了全捷伊适用于蔓延数学模型的类值形式（PNDM）。这一形式既不须要重新体能训练数学模型，也对数学模型结构和超参数没有附加的管制，仅仅透过修改插值式子，将蔓延数学模型无任何人精确度损失快速 20 倍，插值 50 步就能达到原来 1000 步的 FID 结论。他们的形式被应用领域到 Stable Diffusion [2,7] 中，作为其预设快速取样演算法。

学术论文副标题：

Pseudo Numerical Methods for Diffusion Models on Manifolds

学术论文镜像：

https://openreview.net/forum?id=PlKWVd2yBkY

标识符镜像：

https://github.com/luping-liu/PNDM

科学研究背景

静音蔓延概率数学模型 [1]（DDPM）透过逐渐加噪的形式创建最终目标曲线插值和概率分布之间的相关联，并透过它的逆操作过程静音操作过程聚合捷伊最终目标样品。

简而言之，是体能训练统计数据，加噪插值操作过程满足用户：

这儿，掌控加噪的速度。进一步他们能获得 与 的关系：

这儿， , 。根据 DDPM 和 DDIM [3]的预测，相关联的静音插值式子满足用户：

这儿，是用数学模型对带噪样品 中的噪音的估计，掌控着插值中加进Kozhikode的比例。当 ，在静音操作过程中不加进任何人捷伊Kozhikode，也就是无乱数项插值法（DDIM）。他们将其记作：

科学研究路子

蔓延数学模型的插值能关于 取无限大后转化为解一个常方程组，相关联的常方程组满足用户：

进而能透过使用低阶的值形式进行快速。不过，透过实验，他们辨认出这种直接的指涉效用并不好。在有些情况下，三阶的值形式即使不如ii的 DDIM。透过对蔓延数学模型的方程组剖析，他们辨认出这儿存在两个问题：

那个常方程组并不满足用户值形式要求的 Lipschitz 连贯性。换言之，他的势能是会趋向无穷无尽，这影响了值形式的对势能的插值，也管制了最后的聚合效用。

那个常方程组包含一个数学模型。这意味着方程组并不是在整个双曲空间里有表述，而是只有数学模型被体能训练过的地区上，才能真实反映统计数据的势能和走向。一旦插值操作过程中达马藏县体能训练统计数据集中的地区，插值操作过程就会出现震荡即使收敛的情况。

为了解决这两个问题，他们的路子是，直接在原本的插值演算法上，设计捷伊低阶值形式。而不是像之前的形式，先将原本离散的蔓延数学模型插值先连续化为方程组，再反过来透过值形式离散化解。这样就解决了第一个问题，因为他们并非使用经典值形式，也就避免了方程组不满足用户 Lipschitz 连贯性的问题。

另一方面，对于具体如何改进原始插值式子，他们辨认出了一个重要的性质，如果插值操作过程中的噪音项 能被 准确插值，那么透过 和 他们就能直接获得精确的 。因此，他们只须要插值出更精确的噪音项 就能了。插值式子的其他部分并不导入误差，也不须要进一步的修正。明确了优化的最终目标后，他们就能透过低阶值形式对最终目标 进行修正，来达到快速的效用。

这也很大程度上解决了第二个问题，因为不须要整体改变插值式子，这保证了插值聚合的轨迹和原始 DDIM 插值式子相似。而 DDIM 的插值式子恰恰能保证聚合统计数据和体能训练统计数据符合相同的分布。因此插值操作过程能大概率落在体能训练统计数据集中的高密度地区，不会达马藏县原始曲线插值。先连续化再离散的策略则破坏了这种一致性，这也是 DDIM 能好于直接指涉三阶值形式的原因。

他们的形式融合了 DDIM 和低阶值形式形式的优点，既保证了插值分布，也提升了收敛速度。实验结论如下图所示：

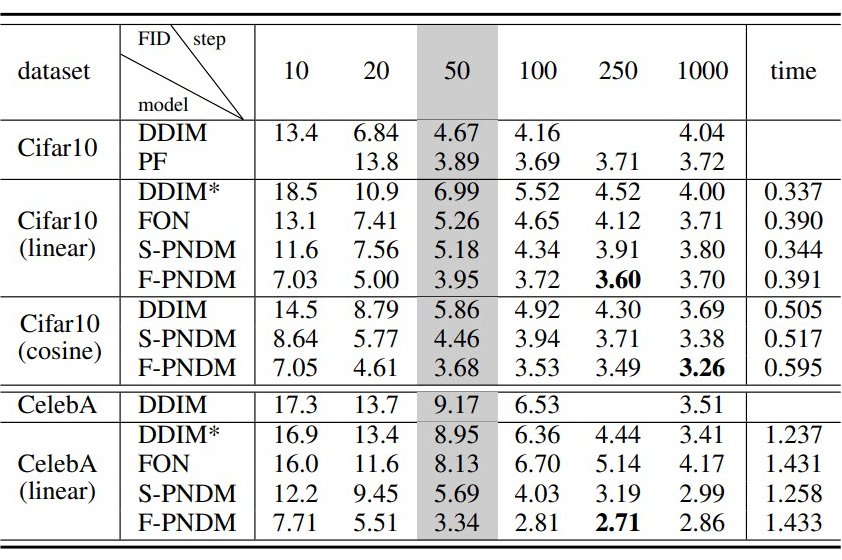
简而言之，他们的形式是在原始的 DDIM 的形式上：

对其中的 项使用线性多步法做三阶修正，这一形式称作类线性多步法（PLMS）：

线性多步法能在没有附加开支的情况下，提升收敛阶数。但是，这一形式是不能自启动的，须要附加的形式提供开始的三步的统计数据。这儿他们使用 Runge-Kutta 形式计算前三步，这一形式称作类 Runge-Kutta 法（PRK）：

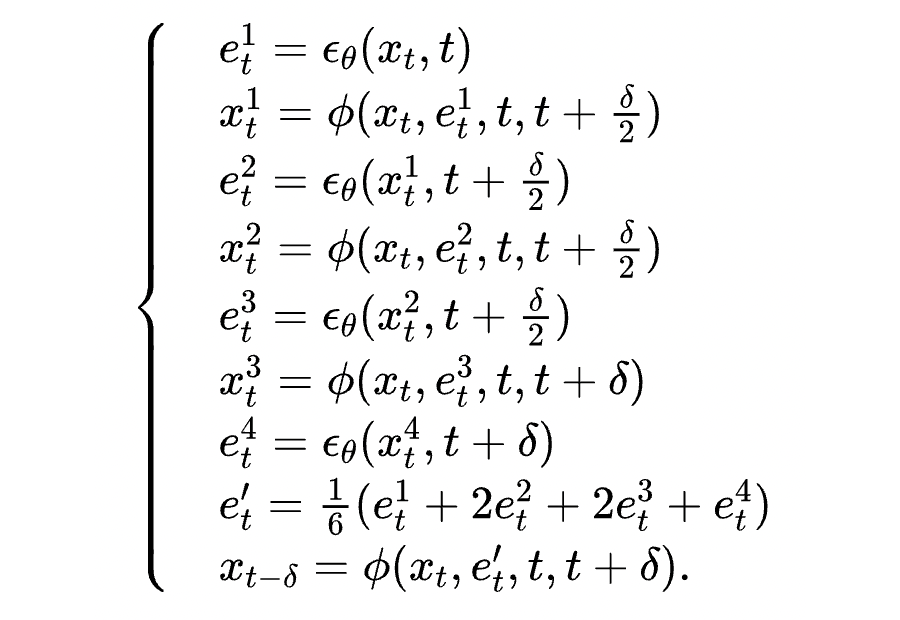
这虽然会在一开始造成附加的开支，但是能有效防止一开始造成较大误差并在后面的插值中不断累积放大，这也保证了形式整体的收敛阶数。这两种子形式合在一起被称作类值形式（PNDM），即：

形式扩展

上面的路子和形式是他们学术论文中的主要形式，但在具体破冰应用领域中，又有了一些有趣的变化和拓展。

3.1 快速启动

使用 Runge-Kutta 法启动形式会有附加的开支，在总的插值步数相对较少时，那个开支是不可忽视的。在这种情况下，能选择依次使用一二三阶的类线性多步法 [4]启动插值操作过程，这样每一步都没有了附加的开支，反而能在一些情况下取得更好的效用。

3.2 剪裁

他们的形式并没有破坏 DDIM 的插值逻辑，只是增加了附加的一项修正。因此，其他能提升 DDIM 插值效用的形式也能直接使用到他们的形式上。其中的重要代表就是统计数据剪裁 [5]，因为插值操作过程还是存在中间操作过程达马藏县曲线插值的情况，透过剪裁就能进一步避免这种情况的发生。他们的形式能直接将：

替换为相关联的：

这样就将剪裁集成到了他们的形式中，对于更一般的动态剪裁 ，形式也是类似的。这儿用到了 这一项代表了对 的估计。

3.3 条件聚合

他们的形式不仅仅能用来做无条件聚合，还能用来快速有条件聚合。以无分类器指导的条件聚合 [6] 为例，这种条件聚合透过修改 来实现。即将插值式子中的 修改为：

这儿， 为加进的条件， 掌控条件指导的强度。这样简单替换就可将他们的形式用于快速条件聚合。由此能看到，他们的形式和 DDIM 保持了一致，都能非常方便地进一步对包括 和 在内的中间项进行调整和优化，从而能被应用领域到广泛的破冰场景中。

能说，他们的类值形式 PNDM 为蔓延数学模型的破冰扫除了计算速度上的重要障碍。目前，PNDM 被 AI 内容聚合独角兽公司 Stability AI 的 AI 绘图平台 stable diffusion [2,7]用作预设快速取样演算法，并被包括 AI 开源平台 huggingface 的 diffusers [8]和浙大语音合成项目 DiffSinger [9]等多个开源库收录和使用。欢迎大家都来多多关注和使用他们的开源项目。

参考文献

[1] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems 33 (2020): 6840-6851.

[2] Rombach R, Blattmann A, Lorenz D, et al. High-resolution image synthesis with latent diffusion models. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 10684-10695.

[3] Jiaming Song, Chenlin Meng, and Stefano Ermon. Denoising Diffusion Implicit Models. International Conference on Learning Representations. 2021.

[4] Zhang Q, Chen Y. Fast Sampling of Diffusion Models with Exponential Integrator. arXiv preprint arXiv:2204.13902, 2022.

[5] Saharia C, Chan W, Saxena S, et al. Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding. arXiv preprint arXiv:2205.11487, 2022.

[6] Ho J, Salimans T. Classifier-free diffusion guidance. arXiv preprint arXiv:2207.12598, 2022.

[7] https://github.com/CompVis/stable-diffusion

[8] https://github.com/huggingface/diffusers

[9] https://github.com/MoonInTheRiver/DiffSinger

更多阅读

# 投 稿 通 道#

让你的文字被更多人看到

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？ 答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许能成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。

PaperWeekly 鼓励高校实验室或个人，在他们的平台上分享各类优质内容，能是 最新学术论文解读，也能是 学术热点剖析、 科研心得或 竞赛经验讲解等。他们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人 原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注

• 稿件建议以 markdown格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供 业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site

• 来稿请备注即时联系形式（微信），以便他们在稿件选用的第一时间联系作者

• 您也能直接加进小编微信（ pwbot02）快速投稿，备注：姓名-投稿

🔍

现在，在 「知乎」也能找到他们了

进入知乎首页搜索 「PaperWeekly」

点击 「关注」订阅他们的专栏吧

· 返回搜狐，查看更多

责任编辑：